Este timpul să privim şi din alt unghi şirul lui Fibonacci. Cunoaştem formula de recurenţă
şi ecuaţia sa caracteristică
care are soluţiile
soluţia pozitivă fiind numărul de aur
Notăm cu
laturile unui dreptunghi şi construim în exterior un pătrat cu latura egală cu lăţimea, iar în dreptunghiul rămas reluăm de o infinitate de ori procedeul. Mai construim şi arcele cu centrul în vârful câte unui pătrat şi care trec prin alte două vârfuri. Ceea ce obţinem se numeşte spirala lui Fibonacci. Laturile fiecărui dreptunghi sunt în tăietură de aur. Fiecare pătrat extras - de exemplu de latură
face să rămână un dreptunghi de laturi
Iată o altă explicaţie a constucţiei spiralei:
- pornim de la dreptunghiul A0B0B1B2, cu laturile în tăietură de aur;
- construim pătratul A0B0A1C;
- diagonala B0B2 intersectează pe A1C în D;
- construim pătratul A1DA2B1, A2 fiind evident pe B1B2;
- diagonala CB1 taie latura DA2 în B3;
- construim pătratul B3A2B2A3, şamd;
- construim acum arcele A0A1, A1A2, A2A3, şamd.
Ştim de ce este numită în continuare "spirala lui Fibonacci", dar dovezile despre această spirală nu apar neaparat din raţiuni matematice.
Universul însuşi, sau poziţia fătului în uter, diferite conexiuni între dimensiuni ale lanţului ADN, sau raportul dintre presiunea sistolică a sângelui şi cea diastolică (apropiat de 1,618), plante sau animale, valurile mării, tornadele.
Vi se pare un mister, nelămurit de generaţii? Nu este doar o coincidenţă cosmică şi nici un standard impus al frumuseţii şi armoniei, ci aşa cum s-a spus "semnătura lui Dumnezeu în creaţie"!



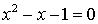
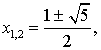








Soțul meu m-a lăsat să fiu cu altDr. Ajayi este un om spiritual puternic la care poți alerga dacă ai nevoie de ajutor, el este vrăjitorul perfect care te poate ajuta să-ți rezolvi problemele vieții. îl poți contacta pe e-mailul lui :drajayi1990@gmail.com și îl poți contacta și pe numărul lui WhatsApp / Viber: +2347084887094 el m-a ajutat să-mi recuperez fosta soție după 4 ani de separare, aveam îndoieli, dar dr. Ajayi a reușit să curgă îndoielile cu rezultate bune. Dr Ajayi pregătește, de asemenea, ierburi pentru orice fel de boală, ierburi pentru a vindeca impotența la bărbați, ierburi pentru a vindeca fibromul, ierburi pentru a rămâne însărcinată, ierburi pentru boli de rinichi, leac pentru diabet și orice fel de problemă de sănătate Dr Ajayi are plante medicinale pentru ele.
RăspundețiȘtergere